Representing Consumption and Saving
Without A Representative Consumer
September 9, 2013
RepresentingWithoutRA.tex
Representing Consumption and Saving
Without A Representative Consumer
September 9, 2013
_____________________________________________________________________________________
Abstract
The Great Recession confirmed a bedrock principle of modern consumption
theory: It is impossible to explain aggregate spending behavior without
knowledge of the underlying microeconomic distribution of circumstances and
choices across households. National accounting frameworks therefore need
to be augmented by “bottom up” measures that both (a) capture the
microeconomic heterogeneity (in expenditures, income, assets, debt, and beliefs)
in the population and (b) sum up to statistics that have a recognizable
relationship to the aggregate totals that are already reasonably well measured.
National Accounting, Inequality, Distribution
D81
| PDF: | http://www.econ2.jhu.edu/people/ccarroll/papers/RepresentingWithoutRA.pdf |
| Slides: | http://www.econ2.jhu.edu/people/ccarroll/papers/RepresentingWithoutRA-Slides.pdf |
| Web: | http://www.econ2.jhu.edu/people/ccarroll/papers/RepresentingWithoutRA/ |
| Archive: | http://www.econ2.jhu.edu/people/ccarroll/papers/RepresentingWithoutRA.zip |
1Contact: ccarroll@jhu.edu, Department of Economics, 440 Mergenthaler Hall, Johns Hopkins University, Baltimore, MD 21218, http://www.econ2.jhu.edu/people/ccarroll, and National Bureau of Economic Research.
One entry in Aristotle’s famous 350 BC catalogue of logical errors is the “Fallacy of Division,” in which the characteristics of a whole are improperly attributed to its parts. A Google search for a contemporary example yields: “America is rich. Z is an American. Therefore Z is rich.”
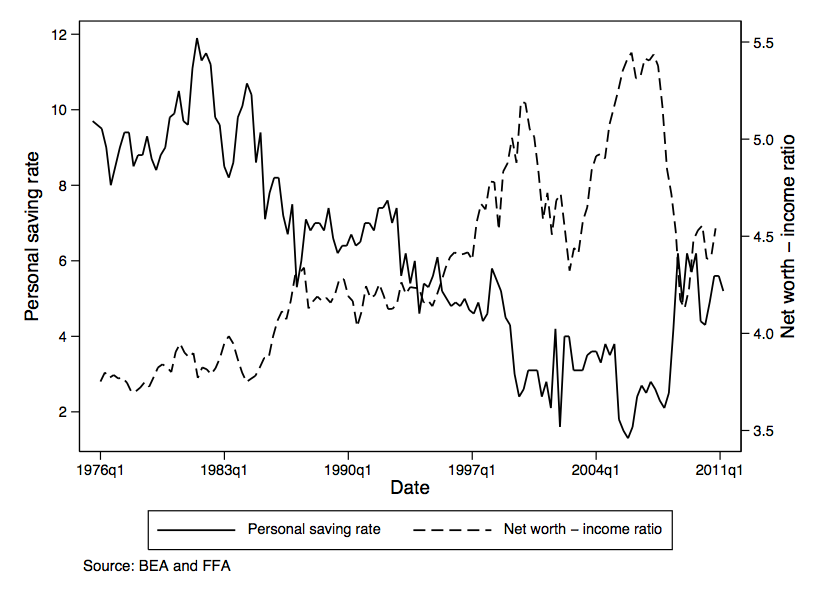
This hits home following an economic crisis widely blamed on an unsustainable runup of household debt. Before the crisis, many macroeconomists (in particular, adherents of the “representative agent” school) argued that the rising debt-to-household-income ratio was nothing to worry about: Aggregate assets had risen more than debt, so the balance sheet of ‘the representative consumer’ was healthy.2 This view was often buttressed by graphical exhibits like Figure 1, which plots total net worth (aggregate assets minus aggregate debt) and personal saving.3 The striking negative relationship between wealth and saving was interpreted as indicating that the low American saving rate was appropriate because, thanks to rising asset prices, the representative consumer’s wealth had increased so much that there was no net need to save (in the aggregate).
The implicit assumption that would justify this conclusion is that debtors and creditors are identical in a key respect: Either group responds to a $1 change in its net wealth by changing annual spending by some small amount like 2 or 3 cents (estimated from aggregate historical data).
Of course, this defies common sense. As James Tobin (1980) remarked long ago in an extended critique of representative agent modeling (cited in International Monetary Fund (2012)), “the population is not distributed between debtors and creditors randomly. Debtors have borrowed for good reasons, most of which indicate a high marginal propensity to spend from wealth or from current income or from any other liquid resources they can command.” And microeconomic evidence has long borne out the proposition that marginal propensities to consume (MPC’s) differ sharply for people with different financial circumstances.
Given these points, it is not surprising that estimated versions of representative agent models did a poor job explaining the collapse in household spending following the crisis. According to one estimate (Carroll, Slacalek, and Sommer (2012)), the drop in wealth can explain only about half of the increase in saving in the crisis.
When economists’ and policymakers’ attention turned to the consideration of fiscal and monetary options to prevent the crisis from turning into a second Great Depression, representative consumer models proved even less useful. Such models gave implausible answers to questions about the likely response of household spending to the main available policy instruments: fiscal ‘stimulus’ measures, and changes in real interest rates. As section 2 of the paper will argue, off-the-shelf representative agent models tend to imply that virtually all of a one-time stimulus check will be saved, a proposition strongly at odds with the microeconomic empirical evidence (from the earliest, e.g. Kreinin (1961) and Friedman (1963), to the latest, e.g. Parker and Broda (2011) and Parker, Souleles, Johnson, and McClelland (2011) (henceforth, PB and PSJM)). Representative agent models also tend to predict that monetary policy should be extremely potent, because according to such models household spending decisions should be hypersensitive to interest rates (a proposition for which there is essentially no empirical evidence at either the micro or the macro level (and not for lack of looking)). A final defect is that off-the-shelf closed-economy representative agent models do not admit any sensible role for the financial sector, really, to exist: The essence of finance is the channeling of funds from those who want to lend to those who want to borrow, but if everyone is identical (as effectively assumed in representative agent models), then everybody follows Polonius’s advice: “Neither a borrower nor a lender be.”4 With neither borrowers or lenders, finance is irrelevant.
Given such manifest inadequacies, why has representative agent modeling been the main tool of macroeconomic analysis for many years? In my view, the answer lies largely in the fact that the data required by representative agent models are easily available, are produced regularly, and are of high quality, while the data necessary to explore more sensible models that take account of microeconomic heterogeneity have mostly been of low quality, are difficult to work with, and (perhaps most importantly) do not paint a picture of the aggregate economy that is consistent with macroeconomic facts that we know from other sources. For example, data from the principal microeconomic survey of household expenditures in the U.S. show a personal saving rate that has been rising steadily for many years, in flagrant contradiction to reasonably well-measured facts from a host of more credible sources (see, e.g., Aguiar and Bils (2011)).
The thesis of this paper is that our only hope of making progress in being able, in real time, to answer questions like “is the recent rapid debt buildup sustainable” or “how would different stimulus plans affect consumer spending” is to augment the existing national accounts with satellite accounts that provide high-quality information at less aggregated levels. Specifically, what is needed is supplementary data that has two characteristics: (a) it is well measured at the level of some microeconomic unit; and (b) it adds up to, or at least makes recognizable contact with, aggregate facts as measured in the existing NIPA accounts. As we shall see, the existing disaggregated data sources satisfy neither of these criteria.
The paper proceeds in three main parts. The first section sketches a modern microfounded framework for saving and balance sheet decisions that I will use to illustrate what will be needed from any expansion of the national accounts that aspires to remedy the problems outlined above. Next comes a precis of the implications of that framework for the measurement of consumption and saving. This provides a natural introduction to a discussion of the problems with existing data sources, as well as to a penultimate section that discusses some promising approaches that are emerging from a variety of nontraditional sources, ranging from personal finance apps to Scandinavian registry data.
Adopting the notational convention that returns on tradable assets accrue
between the end of period 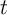 and the beginning of period
and the beginning of period 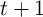 and indexing
the different kinds of such assets by
and indexing
the different kinds of such assets by 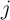 , we can represent the evolution of a
consumer’s balance sheet between the end of period
, we can represent the evolution of a
consumer’s balance sheet between the end of period 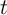 and the ‘decision
moment’ in period
and the ‘decision
moment’ in period 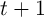 by
by
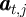 represents the asset positions after all period-
represents the asset positions after all period-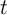 actions have been
accomplished, and the return factor
actions have been
accomplished, and the return factor 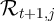 includes interest payments, capital
gains, and depreciation.
includes interest payments, capital
gains, and depreciation. 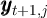 represents the net income in category
represents the net income in category 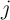 that is
not interpretable as a rate of return; the main example will be cash noncapital
(labor and transfer) income, assigned (arbitrarily) to asset category
that is
not interpretable as a rate of return; the main example will be cash noncapital
(labor and transfer) income, assigned (arbitrarily) to asset category 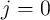 . The
processes of receiving returns and earning income combine to yield a balance
sheet
. The
processes of receiving returns and earning income combine to yield a balance
sheet 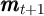 that summarizes the consumer’s market resources at the
moment when consumption and portfolio allocation decisions must be
made.
that summarizes the consumer’s market resources at the
moment when consumption and portfolio allocation decisions must be
made.
It is useful thus to separate these return-and-income-earning processes from
the other steps in the evolution of the household’s balance sheet from an
initial set of values 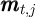 . Using
. Using 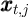 for the net eXpenditures paid out
from a given asset category yields the within-period accounting equation
for the net eXpenditures paid out
from a given asset category yields the within-period accounting equation

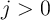 and (assuming that consumption spending is paid for with cash,
which is category 0),
and (assuming that consumption spending is paid for with cash,
which is category 0), 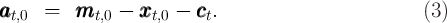
Without a 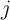 subscript
subscript 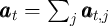 and similarly for
and similarly for 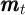 and
and 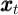 ;
; 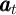 and
and
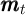 are measures of the household’s total net tradeable wealth position after
and before period
are measures of the household’s total net tradeable wealth position after
and before period 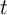 ’s choices of sales and purchases (asset-related net
expenditures
’s choices of sales and purchases (asset-related net
expenditures 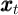 ). Within the period the household’s tradeable net worth thus
evolves according to
). Within the period the household’s tradeable net worth thus
evolves according to
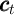 is total expenditures on nondurables and services, and can in principle
be decomposed into arbitrarily many
is total expenditures on nondurables and services, and can in principle
be decomposed into arbitrarily many 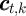 categories that sum to
categories that sum to 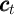 . Note
that rearrangements of the portfolio (selling one asset whose proceeds
are used to buy another) will yield no net contribution to expenditures
. Note
that rearrangements of the portfolio (selling one asset whose proceeds
are used to buy another) will yield no net contribution to expenditures
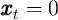 because purchases of one asset are financed by sales of the other
(if there are transactions costs (e.g., brokerage fees) associated with
such rearrangements, those will be captured as a positive net value of
because purchases of one asset are financed by sales of the other
(if there are transactions costs (e.g., brokerage fees) associated with
such rearrangements, those will be captured as a positive net value of
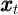 ).5
).5
Using 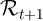 as the portfolio-weighted rate of return, a combination of (4)
and (1) yields an aggregated household-level dynamic budget constraint
as the portfolio-weighted rate of return, a combination of (4)
and (1) yields an aggregated household-level dynamic budget constraint
The key insight of Friedman (1957) was that households’ responses to income shocks ought to depend on whether they perceive those shocks to be transitory or permanent. Since Friedman’s time a vast literature has found that his dichotomy between transitory and permanent shocks provides a good description of household-level income data (for a recent treatment, see Hryshko (2010)). Data also support the proposition that households’ spending response to permanent shocks is much greater than the response to transitory shocks (recently, see Blundell, Pistaferri, and Preston (2008)).
The literature thus suggests that household income dynamics can reasonably be captured by

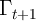 is the growth of permanent income; it incorporates both the
predictable (say, age-related) and the unpredictable (say, receiving tenure (or
not)).
is the growth of permanent income; it incorporates both the
predictable (say, age-related) and the unpredictable (say, receiving tenure (or
not)). 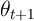 is a mean-one transitory shock.
is a mean-one transitory shock.
Some readers might wonder whether it is wise to impose such a specific description of income dynamics; the answer, gleaned through painful experience, is that even the most basic correlations in cross-section or short-panel empirical data cannot be meaningfully interpreted unless the analyst knows whether the correlation in question is between the object of interest and transitory income, or between that object and permanent income (or at least, some highly persistent component of income that is reasonably approximable by permanent income).6 Some method for distinguishing the transitory from the persistent components of income is therefore entirely appropriate as a requirement for any useful measurement of household balance sheets.
A standard approach to the analysis of consumer behavior is to make the further
assumption that household preferences are time-separable and that the
period utility function is in the Constant Relative Risk Aversion class,
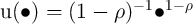 . This specialization to CRRA utility is likely not
necessary for most of the points emphasized below, but will be assumed
henceforth for convenience.
. This specialization to CRRA utility is likely not
necessary for most of the points emphasized below, but will be assumed
henceforth for convenience.
In the CRRA case, the problem can be normalized by permanent income;
using nonbold variables to indicate the corresponding bold variable defined above
so normalized, optimal behavior will be characterized by a consumption function
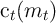 , where the time subscript indicates the dependence of optimal behavior
on age, and the function will differ for each different configuration of
preferences.
, where the time subscript indicates the dependence of optimal behavior
on age, and the function will differ for each different configuration of
preferences.
The decision problem for the household in period 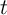 can be written using
normalized variables; the consumer’s objective is to choose consumption function
can be written using
normalized variables; the consumer’s objective is to choose consumption function
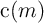 that satisfies:
that satisfies:
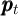 . The only state variable is
(normalized) cash-on-hand
. The only state variable is
(normalized) cash-on-hand 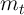 .
.
The principal difference between this framework and typical representative agent models is that household income is assumed to follow a Friedmanesque structure with transitory and permanent shocks whose characteristics are calibrated using microeconomic rather than macroeconomic data.
It is not implausible to expect this calibration to make a big difference, since the estimated variance of permanent shocks to household income in the Panel Study of Income Dynamics is about 100 times as large as the estimated variance of permanent shocks to NIPA disposable personal income (Carroll, Slacalek, and Tokuoka (2011)).7
The generic characteristics of the solution to models like this are captured in
Figure 2, which shows the consumption function for a model described in
Carroll (2011), along with the “sustainable consumption” locus. The place where
the two loci meet defines a “target” such that, if 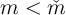 then the cash-on-hand
ratio
then the cash-on-hand
ratio 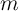 will rise (in expectation), and vice versa if
will rise (in expectation), and vice versa if 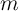 exceeds its
target.
exceeds its
target.
It is worth emphasizing that the target 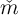 is a ratio of market resources to
permanent income. If at some date
is a ratio of market resources to
permanent income. If at some date 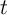 , everyone were at their target
, everyone were at their target 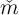 , then
the degree of inequality in the level of market resources
, then
the degree of inequality in the level of market resources 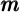 would mirror the
degree of inequality in permanent income
would mirror the
degree of inequality in permanent income 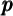 .
.
In practice, the baseline version of the model implies that a set of households
indexed by 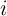 all of whom have identical
all of whom have identical 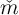 values will have actual
values will have actual
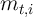 ’s distributed stochastically around that
’s distributed stochastically around that 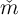 , with the differences
across households attributable to their differing histories of idiosyncratic
shocks. While various nonlinearities in the model prohibit any proof of
an exact correspondence between the model’s implied distribution of
, with the differences
across households attributable to their differing histories of idiosyncratic
shocks. While various nonlinearities in the model prohibit any proof of
an exact correspondence between the model’s implied distribution of
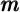 and the simulated population’s distribution of
and the simulated population’s distribution of 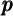 , the intuition
that the baseline model implies a degree of
, the intuition
that the baseline model implies a degree of 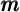 inequality similar to the
degree of
inequality similar to the
degree of 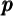 inequality is roughly right. Since any sensible method of
measurement shows a high degree of inequality in permanent income, the
model makes a good start toward explaining the high degree of wealth
inequality measured in the empirical sources like the Survey of Consumer
Finances.
inequality is roughly right. Since any sensible method of
measurement shows a high degree of inequality in permanent income, the
model makes a good start toward explaining the high degree of wealth
inequality measured in the empirical sources like the Survey of Consumer
Finances.
However, Figure 3 (taken from Carroll, Slacalek, and Tokuoka (2011)) shows
that the version of the model in which all households have the same time
preference rate (the ‘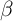 -Point’ version) and thus identical
-Point’ version) and thus identical 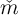 targets produces a
wealth distribution that is far more equal than the actual distribution in the
empirical data (‘U.S. Data’). This reflects the empirical fact that wealth
inequality is much greater than permanent income inequality. Thus, in order for
a model of this kind to match the degree of wealth heterogeneity observed in the
data, it is necessary to introduce some reason for behavioral heterogeneity
beyond simply the fact that different households experience different
shocks.
targets produces a
wealth distribution that is far more equal than the actual distribution in the
empirical data (‘U.S. Data’). This reflects the empirical fact that wealth
inequality is much greater than permanent income inequality. Thus, in order for
a model of this kind to match the degree of wealth heterogeneity observed in the
data, it is necessary to introduce some reason for behavioral heterogeneity
beyond simply the fact that different households experience different
shocks.
Many kinds of heterogeneity are plausible candidates. For example, the model that generated the results in the figure assumes that all agents have the same remaining life expectancy, and the same expected profiles for income growth. Introducing an empirically realistic profile for income over the lifetime and for mortality probabilities would introduce life cycle motives for saving that are absent from that model.
But the literature experimenting with such models is increasingly reaching the conclusion that the vast heterogeneity in outcomes in microeconomic data even among people of the same age and with similar life histories cannot be explained without some degree of heterogeneity in preferences (or, nearly equivalently, in beliefs).
Specifically, the recent macroeconomic literature has begun grudgingly to explore the consequences of differences in characteristics like risk aversion or time preference rates. Preference heterogeneity matters for macroeconomic analysis insofar as it results in an equilibrium in which different consumers have profoundly different responses to any given given shock, so that the distribution of that shock across agents will determine its aggregate impact.
Even without taking a stand on which are the most important kinds of preference heterogeneity for macroeconomics, it is clear that a statistical framework that hopes to represent the data faithfully will need to measure some of the dimensions along which such heterogeneity produces different outcomes. Differences in the structure of households’ balance sheets are likely to be a revealing indicator of differences in their preferences; this by itself would be a compelling reason to measure the structure of household balance sheets, even if there were not other reasons to do so.
It is not hard to see why preference differences might be expected to matter.
Different degrees of patience, or different risk aversion, or differences in many
other kinds of household characteristics should lead households to different
values of 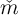 . Since theory implies that macroeconomic outcomes are likely to
depend heavily on the distribution of consumers across values of
. Since theory implies that macroeconomic outcomes are likely to
depend heavily on the distribution of consumers across values of 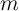 , it seems
inevitable that the distribution of preferences will make a big difference to
macroeconomic predictions.
, it seems
inevitable that the distribution of preferences will make a big difference to
macroeconomic predictions.
Carroll, Slacalek, and Tokuoka (2011) perform a simple experiment to determine whether their baseline model’s failure to fit the degree of inequality can be remedied by the simple expedient of allowing time preference rates to vary across individuals. Although plenty of experimental evidence supports the proposition that time preference rates do differ in the population, their preferred interpretation is that the variation they consider should be viewed proxying also for a host of other kinds of heterogeneity: In age, growth expectations, demographic structure, etc.
Whatever might be the proper interpretation of the estimated degree of time
preference heterogeneity, the solid locus labeled 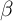 -Dist in figure 3 plots the
results when the distribution of time preference rates in the simulated population
is assumed to be uniform, so that its width can be estimated by a single
parameter. The model targets the proportions of wealth held by the 40th, 60th,
and 80th percentiles in the population, but the model’s simulated distribution
fits the empirical data quite well across the entire spectrum of wealth’s
distribution (except at the very top; the model does not include opportunities for
entrepreneurship, which is the source of much of the income of the richest 1
percent of households).
-Dist in figure 3 plots the
results when the distribution of time preference rates in the simulated population
is assumed to be uniform, so that its width can be estimated by a single
parameter. The model targets the proportions of wealth held by the 40th, 60th,
and 80th percentiles in the population, but the model’s simulated distribution
fits the empirical data quite well across the entire spectrum of wealth’s
distribution (except at the very top; the model does not include opportunities for
entrepreneurship, which is the source of much of the income of the richest 1
percent of households).
The estimated difference in time preference rates between the least and the
most patient agents in the model is only 4 percentage points (at an annual rate).
Nevertheless, the optimal consumption rules of those categories of agents differ
strikingly, as shown in figure 4 (taken from the same source). That figure
also superimposes a histogram of values of 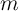 calculated from the 1998
SCF, which shows that a very substantial portion of the population is
concentrated at values of
calculated from the 1998
SCF, which shows that a very substantial portion of the population is
concentrated at values of 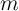 at which impatient households would have a high
MPC.
at which impatient households would have a high
MPC.
One way of evaluating any proposal for how to augment the NIPA accounts to permit better measurement of heterogeneity in saving is by asking whether the resulting data would permit researchers to construct the empirical analogue of figure 4.
Using the notation for a household’s dynamic budget constraint articulated in section 2.1, the data set would need, at a minimum, to contain, for each household:
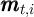 and
and 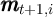
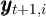
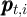
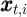
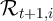
Notably absent from this enumeration is a direct measure of the household’s
consumption expenditures 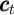 . For reasons articulated below, my proposal is
that consumption should be calculated as a residual; equation (5) can be solved
for
. For reasons articulated below, my proposal is
that consumption should be calculated as a residual; equation (5) can be solved
for 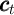 to yield:
to yield:
Considerable value would be gained by having a third year of panel information, so that two successive years of expenditures could be constructed. Friedman (1957) emphasized the importance of accounting for transitory expenditures (a child’s wedding, or unanticipated home repairs after a hurricane) in attempting to assess the validity of his permanent income hypothesis, and although transitory expenditures have not received as much attention as transitory income in the subsequent literature there can be little doubt that they are substantial. Having an extra year (or, better, two) of spending data would allow the analyst to smooth through such episodes.
A further motivation for the collection of several years of consumption data is that standard empirical macroeconomic models today almost all incorporate some form of habit formation in order to capture the substantial degree of sluggishness apparent in aggregate spending dynamics. But to date, the microeconomic literature has found little evidence of habit formation. One interpretation of the lack of microeconomic support for habits, unfortunately, is that the microeconomic data on total household spending are of such poor quality that habit formation may exist but be undetectable using those data. Since a substantial number of important questions in macroeconomic theory, welfare analysis, and public policy depend on whether or not habits exist, the ability to resolve the question by collecting several years’ worth of panel household balance sheet data provides a powerful further motivation for a substantial panel component to any such survey. It seems likely that at least three years’ worth of spending data would be necessary to have a shot at resolving this question, which would require a minimum of four panel wealth interviews. (Though best of all would be an ongoing panel like the Panel Study of Income Dynamics.)
A panel dataset that included only household totals (for example, net worth, total income, and investment transactions) would be an enormous improvement on available data sources. But such a dataset would still be unable to answer some vital questions. A particularly interesting such question at present is the extent to which the internal structure of a household’s balance sheet influences its spending decisions. That is, for a given level of total net market wealth, to what extent (if any) does it matter whether that net worth is held in the form, say, of $100,000 in a bank account versus, say, a house whose value is $600,000 along with a $500,000 mortgage (and cash holdings near zero)? In a world with imperfect capital markets, there are good reasons why the behavior of two such households might be different, including the consequences of house price risk, refinancing risk, risk to various interest rates, and so on. The breakdown of the household’s assets by categories (particularly between debt (secured and unsecured), liquid assets, and illiquid assets) may yield very useful further insights. For example, a recent paper by Kaplan and Violante (2011) argues that even many households with high permanent income have a large proportion of their assets in illiquid forms; they show that if this is the case even households with high wealth-to-income ratios might have a high marginal propensity to consume out of a fiscal stimulus check.
A further reason to probe the allocation of assets across categories is that allocation decisions may yield indirect information about the distribution of household preferences (like the time preference rate). For example, it is easy to show that a household’s degree of risk aversion with respect to investments in risky assets should be directly related to its expected future marginal propensity to consume. (Variation in future returns that does not translate into much variation in future consumption should not generate much risk aversion). Theories about the nature of preference heterogeneity can thus be probed by looking at the interrelationships between net worth, permanent income, consumption, and portfolio allocation. Theories like the ‘hyperbolic discounting’ model of Laibson (1997) that depart from the frictionless optimization paradigm sketched above, may have even stronger predictions for balance sheet structure; for example, Laibson, Repetto, and Tobacman (2007) propose to explain the simultaneous presence of credit card balances and low-return assets on the balance sheets of many households by allowing different short-term and long-term discount factors. It can be argued that the principal reason their view has not been universally adopted is the absence of the kinds of panel data on household balance sheets that can decisively prove that the kinds of behavior they observe in the cross section are not transitory episodes but instead persistently characterize the behavior of the same households over many successive periods.
This paper’s overarching argument is that the household’s dynamic budget constraint is the bedrock on which attempts at microeconomic representations of households’ global choices (like decisions about how much to save, or how to structure a balance sheet between assets and liabilities, or choices about investments in risky versus riskless assets) should rest.
In large part, this view reflects a perception that all other approaches have been tried, and have failed.
A host of existing microeconomic sources attempt to measure slivers of the household’s budget constraint. The CPS, the SIPP, IRS tax panel data, and other sources widely used by labor economists provide a window on households’ incomes but provide little or no information about consumption or assets. The triennial Survey of Consumer Finances has measured the cross section of household balance sheets, but until very recently has provided not provided dynamic (panel) information (the crisis provoked a 2009 reinterview of the 2007 respondents – a valuable, but perhaps unique, experiment).8 The Panel Study of Income Dynamics provides a rich sampling of income data every two years and recently has added considerable data on expenditures, but provides nothing approximating the careful accounting of the evolution of households’ balance sheets that is required for a thorough understanding of saving decisions.
This situation reflects the fact that all of the objects in (5) are difficult to observe. For example, a series of influential papers (e.g. Meyer and Sullivan (2009)) have argued that even income, in principle perhaps the easiest element of the equation to observe, is seriously and systematically mismeasured by existing micro data sources for households in the lower part of the distribution. Given the formidable difficulties in measuring each item, surveys have (reasonably enough) tended to pick one object in the budget constraint for special attention while neglecting the others.
The survey that focuses on the 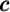 component of the budget constraint
(and neglects the others) is the Consumer Expenditure Survey, which
has been conducted in approximately its current form on a continuous
basis since the early 1980s. Until recently, no other data source
for the U.S. attempted to get much information about household
expenditures.9
component of the budget constraint
(and neglects the others) is the Consumer Expenditure Survey, which
has been conducted in approximately its current form on a continuous
basis since the early 1980s. Until recently, no other data source
for the U.S. attempted to get much information about household
expenditures.9
Unfortunately, the quality of the CE data (like that of data obtained from many other household surveys) has been deteriorating steadily over time. The principal reason for this decline is not hard to guess: Imagine a surveyor arriving at your doorstep and asking “Would you be willing to spend several hours being interviewed about the details of your household spending, and then having us come back and repeat the process four more times over the following year? And, by the way, would you also be willing to keep a complete diary of all of your household’s expenditures for a two-week period?” The number of households contacted who ultimately participate in all five interviews is now only about 40 percent, and no amount of weighting or other statistical wizardry is likely to be able to transform these data into something that is representative of the other households who (understandably) decline to subject themselves to the full course of torture. Furthermore, even among the participating households, there is strong evidence of differential reporting bias; Aguiar and Bils (2011) argue, in particular, that expenditures are differentially underreported by high-income households and that this problem has been growing worse over time, leading (they argue) to serious biases like the survey’s implication that saving rates have increased over time and that consumption inequality has increased less than income inequality.
From the perspective of macroeconomic analysis, perhaps an even more serious problem is the failure of the total spending growth data from the CE survey to show much correlation with macroeconomic aggregates. Attanasio, Battistin, and Padula (2010) show that the correlation of annual changes in expenditures as measured in the CE, and the changes in the corresponding spending categories in the NIPA accounts, is close to zero and statistically insignificant. This result is deeply discouraging for macroeconomists who might want to use CE data to delve into the microfoundations of aggregate fluctuations. If the aggregate fluctuations that are such a prominent feature of the macroeconomic data cannot be reliably detected when the micro data is aggregated, the whole microfoundations research program becomes problematic.10
Recognizing these and other problems, the Bureau of Labor Statistics has recently embarked on an ambitious program to redesign the CE survey from the ground up (see Bureau of Labor Statistics (2011) for an overview). To provide advice, the BLS commissioned a panel of experts (see Horrigan (2010)) from the Committee on National Statistics which issued its report in October of 2012 (see National Research Council (2012)). As in many prior analyses, however, the report was better at documenting the problems of the existing approach than at clarifying how the problems it identifies could be solved.
While the BLS has been commendably open in acknowledging those problems, and has articulated an impressive vision for how to address them,11 it would be a mistake to wait for the CE redesign process to be completed before embarking on an attempt to add disaggregated household satellite accounts to the NIPA data. According to current projections, the CE redesign may not be fully operational for another ten years – assuming it is pursued despite the lean budgets that are likely to prevail in the coming decade. Furthermore, even if the redesigned CE is an improvement in many dimensions on the current survey, there is no guarantee that it will exhibit a major improvement in coherence with NIPA data. The CE survey’s principal statutory purpose is to determine expenditure weights for the Consumer Price Index, and it is possible (perhaps even likely) that the CE redesign might reasonably meet that goal without satisfying the goals articulated above as the chief priorities for NIPA distributional satellite accounts (though see Parker, Souleles, and Carroll (Forthcoming (2014) for an argument that a survey that does not get the totals right cannot be taken seriously as a means of producing weights for the components of those totals).
There is little disagreement with the principle that (5) is the proper framework for accounting for the ‘true’ evolution of a household’s balance sheet. To restate this paper’s main thesis: Extensive and painful experience in trying to learn about the marginal propensity to consume, portfolio choice, the evolution of household balance sheets, and other ‘global’ characteristics of households’ behavior using instruments designed to measure only partial slivers or snapshots of the balance sheet have demonstrably failed. It seems likely at this point that the only approach that offers a reasonable chance of success is one that embraces the dynamic budget constraint rather than ignoring it.
However fervent it may be, an injunction to measure household-level dynamic budget constraints is not likely to be heeded if the task is viewed as impossible. Fortunately, several promising strategies are available.
The most straighforward approach would be to negotiate with the Federal Reserve to expand the scope and mission of its existing Survey of Consumer Finances. The SCF is widely viewed as one of the premier microeconomic surveys in the world, and a deep and broad base of research already exists using the SCF to address a host of important topics.
Most importantly, the economic crisis prompted the Fed to sponsor a reinterview (panel) survey in 2009 of the 2007 respondents, and that reinterview survey could be reinterpreted as a pilot study for the move to a truly panel structure for the SCF.
To achieve the full vision laid out above, the reinterviews would need to become annual, and the sample size would need to be augmented. But if the survey were modified to take advantage of the explosion of personal financial tracking tools available for smartphones and web-based accounts, the burden on respondents might become substantially lighter than in the past.
These considerations also suggest the possibility of designing a new measurement instrument from scratch that could be tailored to the specific needs of the BEA.
I like to think of myself as a public-spirited person. But I shudder at the thought of being asked to participate in the Survey of Consumer Finances or the Consumer Expenditure Survey. Little in modern life appeals less than the idea of than spending hours trying to answer the sorts of questions that make up the substance of such surveys – especially the Consumer Expenditure survey, much of which I could not answer because I simply do not know how much I spent on the various categories of items the survey-takers want to measure.
But my guilt at this reaction is tempered by the self-justifying thought that if the survey takers would be willing to settle for receiving a copy the excellent financial records I keep using personal financial accounting software, I would happily participate. It is hard not to suspect that anyone else who has such records would have the same reaction (though perhaps this reflects a bias identified more recently than 350 BC; modern psycological evidence suggests that individuals tend to think that other people are more like them than those other people actually are).
While the majority of households may not keep such accurate records, it seems plausible that even among people who do not, many would be happy to agree to an offer by the survey taker to organize their financial records for them (in exchange for the surveyor being allowed to keep an anonymized version for research purposes).
A closely related idea would be to contract with one of the proliferating personal finance websites to which millions of people have entrusted their financial account login ID’s and passwords for online access. These “aggregator” sites then construct balance sheets for their customers that incorporate many of the elements needed for BEA’s purposes. Such sites are typically free, paid for with advertising revenue. It seems that it would be a short leap for the BEA to advertise for volunteers on such a site, at least for a pilot project to see how much could be learned from such a source.
Another starting point might be to approach the firms that constitute the “wealth management” industry, who have developed their own systems for measuring the household balance sheets of their customers. The software systems used by firms in this industry are more focused on capturing the complex details of the balance sheets of wealthy households than on measuring details of spending, so an approach that began with wealth management software would probably need to be augmented for some method of constructing a reasonably reliable measure of expenditures as well, but again a customized version of the software could surely be commissioned for this purpose.
Any of these strategies would of course require efforts to deal with the obvious sample selection problems reflected in the fact that the users of personal finance software or websites (or wealth management services!) are not a random sampling of the population. It is not obvious, however, that these sampling problems are more difficult than the crippling problems already afflicting many surveys. Indeed, it is not at all implausible to suppose that many respondents would be pleased to receive free software and training in exchange for release of their (anonymized) financial information.
A number of Scandanavian countries have undertaken initiatives to pull together all of their governments’ records about individual citizens into a single database. The amalgamated dataset includes tax and property records, demographic information, earnings, and a smorgasbord of other information.
In Sweden, as a legacy of a now-abolished weath tax, the national database even includes highly detailed data on real estate values, mortgage debt, and financial information, including security-by-security transactions data. A fascinating recent paper by Koijen, Nieuwerburgh, and Vestman (2013) pulls together these data to construct a measure of household expenditures along precisely the lines sketched above (proving, if nothing else, that such a scheme is practical enough to be implemented, at least in Sweden). Of the many interesting results in the paper, one stands out: The correlation is not particularly high between expenditures as measured in this way, and expenditures measured using a traditional expenditure survey (respondents’ answers are linkable to their national registry records). Since the authors have high quality data on virtually every component of the dynamic budget constraint as specified above, these results suggest that the expenditure survey data are of even lower quality than one might have hoped. (See also the related paper by Kreiner, Lassen, and Leth-Petersen (2013) on a similar exercise Danish registry data, which does not contain wealth transactions information).
Of course, the BEA needs to measure balance sheets in the U.S., not Sweden. But the existence of the Scandinavian registry data could nevertheless be useful in several ways. First, joint initiatives with such countries could provide an invaluable way for the BEA to answer many questions whose resolution might be nearly impossible in the U.S. (such as determining which questions, if any, households can accurately answer in a survey context). Second, sponsored research (either jointly between BEA and the other country’s statistical bureau, or by academic researchers with access to the data) could explore the extent to which data of this kind really satisfy the needs of the BEA. A particular question that could be addressed is the extent to which measures of aggregate expenditures constructed using the balance sheet approach resemble spending dynamics obtained using traditional methods like retail sales surveys. Another target would be to match aggregate Flow of Funds accounts.
If research of this kind demonstrated that administrative data are the “holy grail” of national income statistics, perhaps progress could be made in moving toward a similar system in the U.S. At present, privacy rules and other impediments have prevented the kinds of data sharing across government agencies that has allowed the Swedes (and the Danes, and Norwegians) to construct their impressive databases. With concerted and sustained efforts (and careful rules about privacy), it is possible that many of these rules could be relaxed for the purpose of producing anonymized national accounts data.
An alternative might be to combine such adminstrative data with survey data. This could be done either by compiling a large database of administrative data and then sampling the households in that dataset to ask the crucial questions needed to fill out the balance sheets; or the approach could be the inverse: Begin with transactions data from an online or personal finance source, then augment those with administrative data.
One key contribution that administrative data might be able to make in either of these cases would be to help in constructing a measure of permanent income for the individuals constituting a household. Social Security earnings histories could be enormously helpful in measuring permanent income, which is unlikely to be easy to measure using the time-limited data that can be obtained using either of the other approaches.
If the purpose of national accounts is to provide the data needed to understand the workings of the economy at the aggregate level, it seems clear that this mission is not satisfactorily accomplished by the existing NIPA accounts. Both economic theory and practical experience indicate that detailed microeconomic information on household balance sheets and their dynamics will be essential for making progress. While the challenge is formidable, a variety of recent developments suggest it is not infeasible. The remarkable data available in Scandinavian countries provide a testbed for research on the measurement of balance sheets. Recent advances in electronic data resources, along with the successful recent reinterview survey by the Survey of Consumer Finances, point to alternative paths for accomplishing the goal in the U.S.
If a successful set of satellite accounts on the distribution and evolution of household balance sheets could be constructed, that would constitute arguably the most important advance in national income accounting since the glory days of the 1950s, when the accounts were first created in their present form. It is a big challenge, and one that will require collaboration with academia, with other countries, and with the private sector (as happened in the 1950s). But it is a challenge that has the potential to make national accounting exciting in a way that has not been true for 50 years.
AGUIAR, MARK A., AND MARK BILS (2011): “Has Consumption Inequality Mirrored Income Inequality?,” NBER Working Paper 16807, National Bureau of Economic Research, Inc.
ARISTOTLE (350 BC): On Sophistical Refutations. The Wikipedia Foundation.
ATTANASIO, ORAZIO, ERICH BATTISTIN, AND MARIO PADULA (2010): Inequality in Living Standards Since 1980: Evidence from Expenditure Data. American Enterprise Institute.
BLUNDELL, RICHARD, LUIGI PISTAFERRI, AND IAN PRESTON (2008): “Consumption Inequality and Partial Insurance,” American Economic Review, 98(5), 1887–1921.
BUREAU OF LABOR STATISTICS (2011): “Consumer Expenditure Survey (CE) Gemini Project,” .
CARROLL, CHRISTOPHER D. (2011): “Theoretical Foundations of Buffer Stock Saving,” Manuscript, Department of Economics, Johns Hopkins University, http://www.econ2.jhu.edu/people/ccarroll/papers/BufferStockTheory.
CARROLL, CHRISTOPHER D., JIRI SLACALEK, AND MARTIN SOMMER (2012): “Dissecting Saving Dynamics: Measuring Wealth, Precautionary, and Credit Effects,” Manuscript, Johns Hopkins University, http://www.econ2.jhu.edu/people/ccarroll/papers/cssUSSaving/.
CARROLL, CHRISTOPHER D., JIRI SLACALEK, AND KIICHI TOKUOKA (2011): “Digestible Microfoundations: Buffer Stock Saving in a Krusell-Smith World,” Manuscript, Johns Hopkins University, At http://www.econ2.jhu.edu/people/ccarroll/papers/BSinKS.pdf.
DEBACKER, JASON, BRADLEY HEIM, VASIA PANOUSI, SHANTHI RAMNATH, AND IVAN VIDANGOS (2013): “Rising Inequality: Transitory or Permanent? New Evidence from a Panel of US Tax Returns,” mimeo.
FRIEDMAN, MILTON A. (1957): A Theory of the Consumption Function. Princeton University Press.
__________ (1963): “Windfalls, the ‘Horizon,’ and Related Concepts in the Permanent Income Hypothesis,” in Measurement in Economics, ed. by Carl Christ, pp. 1–28. Stanford University Press.
HIMMELBERG, CHARLES, CHRISTOPHER MAYER, AND TODD SINAI (2005): “Assessing High House Prices: Bubbles, Fundamentals and Misperceptions,” Journal of Economic Perspectives, 19(4), 67–92.
HORRIGAN, MICHAEL (2010): “Official Charge to the CNSTAT Panel on Redesign of the Consumer Expenditure Survey,” .
HRYSHKO, DMYTRO (2010): “RIP to HIP: The Data Reject Heterogeneous Labor Income Profiles,” Manuscript, University of Alberta; forthcoming, Quantitative Economics.
INTERNATIONAL MONETARY FUND (2012): World Economic Outlook, 2012chap. 3. International Monetary Fund, Available at http://www.imf.org/external/pubs/ft/weo/2012/01/pdf/text.pdf.
KAPLAN, GREG, AND GIOVANNI L. VIOLANTE (2011): “A Model of the Consumption Response to Fiscal Stimulus Payments,” NBER Working Paper Number W17338.
KOIJEN, RALPH, S. VAN NIEUWERBURGH, AND ROINE VESTMAN (2013): “Judging the Quality of Survey Data by Comparison with Truth as Measured By Administrative Records: Evidence from Sweden,” in Forthcoming in Improving the Measurement of Household Expenditures. Chicago: University of Chicago Press.
KREINER, CLAUS THUSTRUP, DAVID DREYER LASSEN, AND SØREN LETH-PETERSEN (2013): “Examples of Combining Administrative Records and Survey Data in Validation Studies,” in Improving the Measurement of Household Expenditure. University of Chicago Press, http://www.nber.org/confer/2011/CRIWf11/Leth-Petersen.pdf.
KREININ, MORDECAI E. (1961): “Windfall Income and Consumption: Additional Evidence,” American Economic Review, 51, 388–390.
KRUGMAN, PAUL (2005): “That Hissing Sound,” New York Times Column.
LAIBSON, DAVID (1997): “Golden Eggs and Hyperbolic Discounting,” Quarterly Journal of Economics, CXII(2), 443–477.
LAIBSON, DAVID, ANDREA REPETTO, AND JEREMY TOBACMAN (2007): “Estimating Discount Functions with Consumption Choices over the Lifecycle,” Working Paper 13314, National Bureau of Economic Research.
MEYER, BRUCE D., AND JAMES X. SULLIVAN (2009): “Five Decades of Consumption and Income Poverty,” Working Papers, Harris School of Public Policy Studies, University of Chicago.
NATIONAL RESEARCH COUNCIL (2012): Measuring What We Spend: Toward a New Consumer Expenditure Survey. The National Academies Press, Don A. Dillman and Carol C. House, Editors; Panel on Redesigning the BLS Consumer Expenditure Surveys; Committee on National Statistics; Division of Behavioral and Social Sciences and Education.
PARKER, JONATHAN, AND CHRISTIAN BRODA (2011): “The Economic Stimulus Payments of 2008 and the Aggregate Demand for Consumption,” Manuscript, Northwestern University.
PARKER, JONATHAN A., NICHOLAS SOULELES, AND CHRISTOPHER D. CARROLL (Forthcoming (2014)): “The Benefits of Panel Data in Consumer Expenditure Surveys,” in Improving the Measurement of Household Expenditures, ed. by Christopher D. Carroll, Thomas Crossley, and John Sabelhaus. University of Chicago Press, At http://www.econ2.jhu.edu/people/ccarroll/papers/ParkerSoulelesCarroll/.
PARKER, JONATHAN A., NICHOLAS S SOULELES, DAVID S. JOHNSON, AND ROBERT MCCLELLAND (2011): “Consumer Spending and the Economic Stimulus Payments of 2008,” NBER Working Papers 16684, National Bureau of Economic Research, Inc.
PARKER, JONATHAN A., AND ANNETTE VISSING-JORGENSEN (2009): “Who Bears Aggregate Fluctuations and How?,” NBER Working Papers 14665, National Bureau of Economic Research, Inc.
SHILLER, ROBERT (2005): “Yale Professor Predicts Housing ‘Bubble’ Will Burst,” Interview with National Public Radio.
TOBIN, JAMES (1980): Asset Accumulation and Economic Activity: Reflections on Contemporary Macroeconomic Theory. Basil Blackwell.