The Ramsey/Cass-Koopmans (RCK) Model

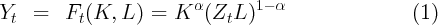
^©April 15, 2008, Christopher Carroll RamseyCassKoopmans

This handout presents the Ramsey (1928)/Cass (1965)-Koopmans (1965) (RCK) model in continuous time for an economy with exogenous labor-augmenting technological progress.

1 The Model

The economy has a perfectly competitive production sector that uses a Cobb-Douglas aggregate production function

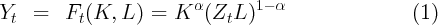
Y = F (K, L) = K α (Z L )1- α (1) t t t

to produce output using capital and labor; labor supply (the same as population) increases exogenously at a constant rate

˙ L ∕L = n (2)

and Z is an index of labor productivity that grows at rate

Z˙ ∕Z = g. (3)

Thus, technological progress allows each worker to produce more and more as time goes by with the same amount of physical capital (this is the definition of labor-augmenting technical progress). The quantity ZL is known as the number of ‘efficiency units’ of labor in the economy.

Suppose that there is a social planner whose goal is to maximize the discounted sum of CRRA utility from per-capita consumption:

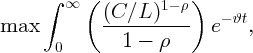∫ ∞ ( 1- ρ) max (C-∕L-)---- e- ϑt, 0 1 - ρ

(4)

subject to

K˙ = Y - C - δK. (5)

Now define lower case variables as the upper case version divided by efficiency units, i.e.

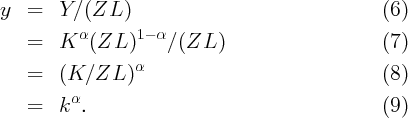
y = Y ∕ (ZL ) (6) α 1- α = K (ZL ) ∕(ZL ) (7) α = (K ∕ZL ) (8) = k α. (9)

Note that

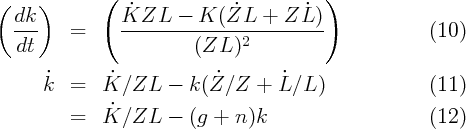
( ) ( ) dk- K˙ZL-------K-(Z˙L---+-Z-L˙)- = 2 (10) dt (ZL ) ˙ ˙ ˙ ˙ k = K ∕ZL - k (Z ∕Z + L ∕L ) (11) ˙ = K ∕ZL - (g + n )k (12)

which means that (5) can be divided by ZL and becomes

˙ K ∕ZL = y - c - δk (13) ˙k + (g + n )k = f (k) - c - δk (14) ˙k = f (k) - c - (g + n + δ)k. (15)

This definition also means that C∕L = Z(C∕ZL) = Zc. Recalling now that for a variable growing at rate g

Z = Z egt (16) t 0

we can rewrite

C ∕L = cZ (17) gt = cZ0e (18)

which implies that we can rewrite the social planner’s objective function as

∫ ( ) ∫ ( ) ∞ (Zc )1- ρ 1- ρ ∞ c1- ρ --------- e- ϑt = Z 0 ------- e- ϑte (1- ρ)gt (19) 0 1 - ρ 0 1 - ρ ∫ ∞ = Z10- ρ u(c)e ((1- ρ)g- ϑ)t. (20) 0

Thus, defining ν = ϑ - (1 - ρ)g and normalizing the initial level of productivity to Z₀ = 1, the complete optimization problem can be formulated as

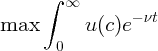∫ ∞ - νt max u(c )e 0

(21)

subject to

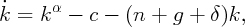˙k = kα - c - (n + g + δ)k,

(22)

which has a discounted Hamiltonian representation

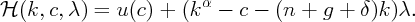α H (k, c,λ ) = u(c) + (k - c - (n + g + δ)k )λ.

(23)

The first discounted Hamiltonian optimization condition requires ∂∕∂c = 0:

- ρ c = λ (24) - ρc - ρ- 1˙c = ˙λ (25)

The second discounted Hamiltonian optimization condition requires:

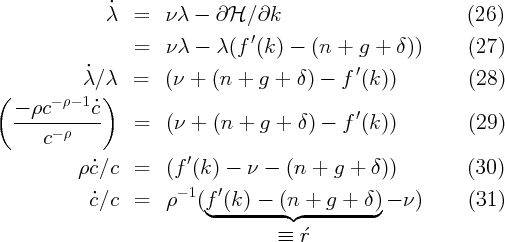
λ˙ = νλ - ∂H ∕∂k (26) ′ = νλ - λ (f (k) - (n + g + δ )) (27) ˙ ′ ( λ ∕λ) = (ν + (n + g + δ) - f (k )) (28) - ρc- ρ- 1c˙ ′ ------ρ---- = (ν + (n + g + δ) - f (k )) (29) c ρ˙c∕c = (f′(k) - ν - (n + g + δ )) (30) ˙c∕c = ρ- 1 (f′(k) - (n + g + δ )- ν ) (31) ◟--------◝ ◜---------◞ ≡ r´

where the definition of ŕ is motivated by thinking of f^′(k) - (n + g + δ) as the interest rate net of depreciation and dilution.

This is called the “modified golden rule” (or sometimes the “Keynes-Ramsey rule” because it was originally derived by Ramsey with an explanation attributed to Keynes). (The unmodified “golden rule” optimality condition amounts to this equation with the time preference rate set to ϑ = 0, and was proposed by Phelps (1961), an article well worth reading; this is one of the chief contributions for which Phelps won the Nobel prize.)

Thus, we end up with an Euler equation for consumption growth that is just like the Euler equation in the perfect foresight partial equilibrium consumption model, except that now the relevant interest rate can vary over time as f^′(k) varies.

Substituting in the modified time preference rate gives

c˙∕c = ρ- 1(f ′(k ) - (n + δ + g) - ϑ + (1 - ρ)g ) (32) - 1 ′ = ρ (f (k ) - (n + δ) - ϑ - ρg), (33)

and finally note that defining per capita consumption χ = C∕L so that c = χZ^-1,

˙- 1 - 1 - 1 ˙ c˙ = (χZ ) = χ˙Z - (χZ )Z ∕Z (34) ˙c∕c = χZ ˙- 1∕(χZ - 1) = ˙χ ∕χ - g (35)

and since (33) can be written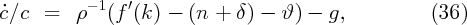

- 1 ′ c˙∕c = ρ (f (k ) - (n + δ) - ϑ) - g, (36)

we have

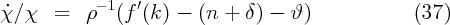
˙χ∕ χ = ρ - 1(f ′(k ) - (n + δ ) - ϑ ) (37)

so the formula for per capita consumption growth (as a function of k) is identical to the model with no growth (equation (33) with g = 0). Any important differences between the no-growth model and the model with growth therefore must come through the channel of differences in k.

2 The Steady State

The assumption of labor augmenting technological progress was made because it implies that in steady-state per-capita consumption, income, and capital all grow at rate g.

ċ∕c = 0 implies that at the steady-state value of ¯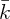
k

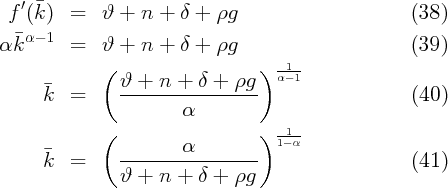
f ′(¯k ) = ϑ + n + δ + ρg (38) ¯α- 1 α k = ϑ + n + δ + ρg (39) ( ) α1-1 ¯ ϑ-+--n-+--δ-+-ρg-- k = α (40) ( ) -1- α 1- α ¯k = ------------------ (41) ϑ + n + δ + ρg

Thus, the steady-state k will be higher if capital is more productive (α is higher), and will be lower if consumers are more impatient, population growth is faster, depreciation is greater, or technological progress occurs more rapidly.

3 A Phase Diagram

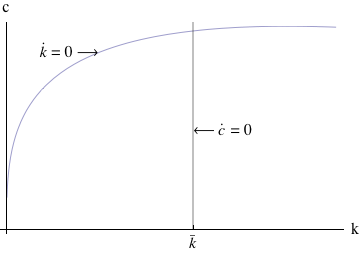
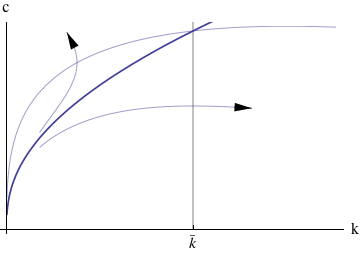
While the RCK model has an analytical solution for its steady-state, it does not have an analytical solution for the transition to the steady-state. The usual method for analyzing models of this kind is a phase diagram in c and k.

The first step in constructing the phase diagram is to take the differential equations that describe the system and find the points where they are zero. Thus, from (15) we have that = 0 implies

c = f (k) - (g + n + δ )k (42)

and we have already solved for the (constant)

that characterizes the ċ∕c = 0 locus. These can be combined to generate the borders between the phases in the phase diagram, as illustrated in figure 1.

4 Transition

Actually, as stated so far, the solution to the problem is very simple: The consumer should spend an infinite amount in every period. This solution is not ruled out by anything we have yet assumed (except possibly the fact that once k becomes negative the production function is undefined).

Obviously, this is not the solution we are looking for. The problem is that we have not imposed anything corresponding to the intertemporal budget constraint. In this context, the IBC takes the form of a “transversality condition,”

∫t lim λte (g+n)t- 0 rτdτkt = 0. (43) t→ ∞

The intuitive purpose of this unintuitive equation is basically to prevent the capital stock from becoming negative or infinity as time goes by. Obviously a capital stock that was negative for the entire future could not satisfy the equation. And a capital stock that is too large will have an arbitrarily small interest rate, which will result in the LHS of the TVC being a positive number, again failing to satisfy the TVC.

Figure 2 shows three paths for c and k that satisfy (33) and (15). The topmost path, however, is clearly on a trajectory toward zero then negative k, while the bottommost path is heading toward an infinite k. Only the middle path, labelled the “saddle path,” satisfies both (33) and (15) as well as the TVC (43).

References

Cass, David (1965): “Optimum growth in an aggregative model of capital accumulation,” Review of Economic Studies, 32, 233–240.

Koopmans, Tjalling C. (1965): “On the concept of optimal economic growth,” in (Study Week on the) Econometric Approach to Development Planning, chap. 4, pp. 225–87. North-Holland Publishing Co., Amsterdam.

Phelps, Edmund S. (1961): “The Golden Rule of Accumulation,” American Economic Review, pp. 638–642.

Ramsey, Frank (1928): “A Mathematical Theory of Saving,” Economic Journal, 38(152), 543–559.

Appendix: Numerical Solution

The RCK model does not have an analytical solution, which means that numerical methods must be used to find out the model’s quantitative implications for transition paths.

The method of solution of these kinds of models is not important for the purposes of first year graduate macroeconomics; this appendix has been written as a reference for more advanced students who might be beginning their research on growth models.

The most effective method of numerical solution is called the ‘time elimination’ method. It starts from the fact that

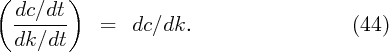
( ) dc-∕dt- = dc∕dk. (44) dk ∕dt

Note from (33) that we can write

c˙ = ρ - 1(f ′(k) - ϑ - (n + δ ) - ρg )c, (45)

so we can obtain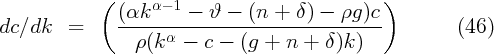

( ) (αk-α-- 1---ϑ---(n--+-δ-) --ρg-)c dc ∕dk = α (46) ρ (k - c - (g + n + δ)k )

which is a differential equation with no analytical solution. However, many numerical math packages can solve differential equations numerically, yielding a numerical version of the c(k) function.

There is one problem, however, which is that at the steady-state values of c and k both numerator and denominator of this equation are zero. We could use L’Hopital’s rule to derive an expression in this neighborhood, but that gets very messy. The alternative is to solve the differential equation twice: Once for a domain extending from k = 0 to 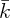- ε, yielding c_-(k), and once for a domain from 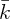+ ε to some large value of k, yielding c₊(k). The true consumption policy function can then be approximated by interpolating between the upper endpoint of c_-(k) and the lower endpoint of c₊(k).

Figure 1:

ċ∕c = 0 and ˙
k

= 0 Loci

Figure 2:

Transition to the Steady State